Exemple de mise en œuvre de la prise en compte d’incertitudes

Nous allons ici déterminer la valeur d’un mesurande S, en déterminant une valeur a=β*Sⁿ (où β est une constante) qui est :

· fonction d’un couple de deux mesurandes primaires (X_i , Y_i ) avec autant de valeurs de couples (X_i , Y_i) possibles que nous aurons fait de mesures {Tous les couples, différents, visent à cerner une même valeur de a},

· fonction telle que a = (Y_i – b)/ X_i , i.e. Y_i =a* X_i + b où b est une constante (à laquelle nous laisserons donc la possibilité d’être non nulle).

L’intérêt de réaliser plusieurs mesures de couples (de valeurs X_i et Y_i différentes pour chacun des couples) réside dans le fait que chacune des valeurs X_i et Y_i est comme il se doit affublée d’une incertitude de mesure : un plus grand nombre de mesures permettra d’estimer une meilleure incertitude de mesure sur a, et donc sur S.

Ce mode de détermination sera appliqué à une distance d (S est alors d, et nous verrons que n=2) séparant deux plaques formant un condensateur.

Nous déduirons de la valeur de d affublée de son incertitude, une capacité C également affublée de sa propre incertitude.

Dans le montage expérimental suivant

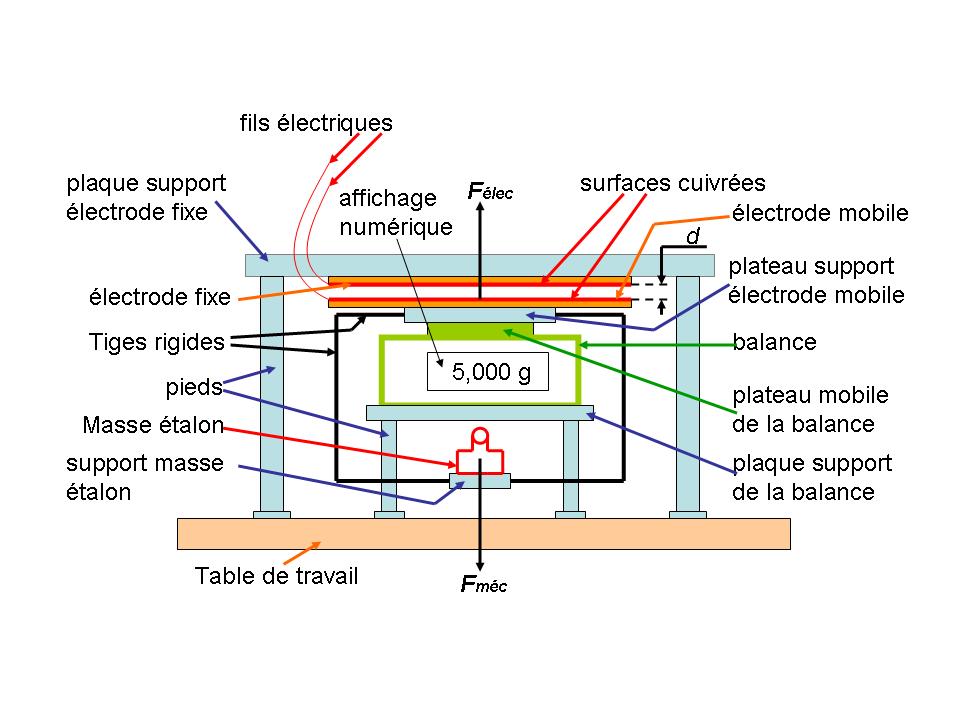
où nous distinguons:

- deux plaques rectangulaires identiques pour circuits imprimés, vierges (donc entièrement recouvertes d’une surface cuivrée), supposées parfaitement planes, de largeur L et de longueur l, formant un condensateur plan-plan de capacité C,

- une balance à affichage numérique dont la résolution est égale à 1 mg (dernier chiffre significatif),

- une masse étalon M,

- divers éléments mécaniques : plaques et plateaux supports, pieds, tiges rigides,

- des fils électriques de connexion souples (reliés à une alimentation haute tension stabilisée ajustable qui n’est pas représentée), polarisant le condensateur sous une haute tension U (par exemple en branchant le fil soudé à la plaque de dessous à la masse et celui soudé à la plaque de dessus à une tension U),

et où, au départ, alors que la tension V₀ entre les fils électriques est égale à zéro et qu’aucune masse n'est déposée sur le plateau inférieur :

- a été effectuée une tare (remise à zéro) de la balance qui supporte (sur son plateau mobile) les différents éléments mécaniques tels l'électrode mobile, son support, les tiges rigides et le petit plateau inférieur,

- la balance affiche donc 0,000 g et l'électrode mobile se trouve à une distance "d" dont on cherchera à déterminer la valeur ainsi que son écart-type,

il s’établit, quand une masse M est déposée sur le plateau inférieur, par expression de l’égalité entre la force d’attraction entre les plaques du condensateur et la force gravitationnelle exercée sur M, que :

d = U.( e₀.l.L / (2M.g))^1/2

i.e. U=d*(2g/(e₀.l.L))^1/2* M^1/2

Ici, Y_i=U^², X_i=M, a= d²*2g/(e₀.l.L), et b est, a priori, 0 (a priori car cela est le cas seulement si l’expérience est totalement conforme avec la formule théorique de d).

Inventaire des grandeurs :

Unités pour chacune des lignes	Grandeurs	Valeurs	σ
V	U		1
mm	l	200	0,5
mm	L	300	0,5
F.m-1	e0	8,8542E-12	0
g	M		0,0003
m/s^2	g	9,8094	0

Et (σ_d / d)² = (σ_U / U )² + (σ_l / 2.l)² + (σ_L / 2.L)² + (σ_M / 2.M)²

Nous plaçons ensuite successivement les masses suivantes sur le plateau inférieur (en vérifiant la valeur de l’indication numérique donnée par la balance) ; et en ajustant, pour chacune de ces valeurs, la tension U, nous annulons la somme de la force exercée par chaque masse et de la force électrostatique.

M_i = 0,5 g, 1 g, 2 g, 3 g, 4 g, 5 g, 6 g, 7 g, 8 g, 9 g et 10 g :

Ui (V)	Mi (g)	Ui^^2 (V²)
172,6	0,500	29790,76
249,3	1,000	62150,49
349,9	2,000	122430,01
440,5	3,000	194040,25
510,7	4,000	260814,49
573,2	5,000	328558,24
641,0	6,000	410881,00
709,0	7,000	502681,00
758,0	8,000	574564,00
799,0	9,000	638401,00
839,0	10,000	703921,00

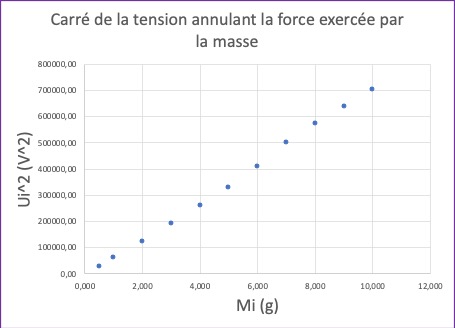
Si la droite de régression du nuage de N points (M, U²)=(x_i,y_i) est y=b+ax,

a=(1/Δ)*(NΣx_i y_i -Σx_i Σy_i) et b=(1/Δ)*(Σx_i²Σ y_i -Σx_i Σ x_i y_i),

où Δ=NΣx_i²-(Σx_i)²

(Pour rappel, ceci s’obtient tout simplement en annulant les dérivées, par rapport à a et à b, de Σ( y_i- b-ax_i)²)

Mise en œuvre :

Mi (g)	Mi (Kg)=xi	Ui (V)	Ui^2 (V²)=yi
0,500	0,0005	172,6	29790,76
1,000	0,001	249,3	62150,49
2,000	0,002	349,9	122430,01
3,000	0,003	440,5	194040,25
4,000	0,004	510,7	260814,49
5,000	0,005	573,2	328558,24
6,000	0,006	641,0	410881,00
7,000	0,007	709,0	502681,00
8,000	0,008	758,0	574564,00
9,000	0,009	799,0	638401,00
10,000	0,01	839,0	703921,00

Σxi^2	0,00038525	Kg*Kg
(Σxi)^2	0,003123161	Kg*Kg
Δ	0,001114589	Kg*Kg
Σxi Σyi	212466,8893	Kg*V²
Σxi yi	26955,4598	Kg*V²
a	75402844,56	V²/Kg
b	-19021,85615	V²

axi (V²)	yi- b-axi (V²)
37701,42228	11111,2
75402,84456	5769,5
150805,6891	-9353,8
226208,5337	-13146,4
301611,3782	-21775,0
377014,2228	-29434,1
452417,0674	-22514,2
527819,9119	-6117,1
603222,7565	-9636,9
678625,601	-21202,7
754028,4456	-31085,6

σy= ((1/(N-2))* Σ( yi- b-axi)^2)^1/2	20576,784	V²
σa= σy* (N/Δ)^1/2	2044167,587	V²/Kg

(Formules, notamment la seconde, tirée(s) d’un livre du Pr John Taylor, Dept of Physics, Univ of Colorado)

D’où a=75 (2) 10^6 V^2/Kg

{Remarque :

Excel donne a= 72607488,97 V²/ Kg ^$$

et une valeur de la moitié de la différence des limites sup et inf, pour un seuil de confiance de 95%, égale à 2340324,52 V²/Kg ^$$$,

i.e. : a=73 (2) 10^6 V²/ Kg : les 2 « méthodes » ne s’opposent pas, puisque les 2 résultats se recouvrent.

$$ : Valeur donnée dans la cellule « [Variable X 1 ; Coefficients] »

du tableau du rapport détaillé obtenu en demandant une régression linéaire à partir de l’item « Outils d’analyse » en ayant sélectionné les données [Mi (en Kg) = xi ; Ui^2 (en V²) = yi].

$$$ : La moitié de la différence des limites en question explicitement désignées dans le même tableau.

}

Nous allons pouvoir accéder à la valeur de d par d = U.( e₀.l.L / (2.M.g))^1/2 =(( e₀.l.L / (2 g))*U²/M)^1/2

i.e. d=a^1/2.( e₀.l.L / (2.g))^1/2

Avec la valeur de a calculée ci-dessus :

A.N. : d=1,428920E-03 m (Résultat temporaire en attendant d’estimer σ_d)

Avec la valeur de σ_a calculée ci-dessus :

σ_d = d[(σ_a / 2.a )² + (σ_l / 2.l)² + (σ_L / 2.L)²]^(1/2)

A.N. : σ_d = 1,948757E-05 m

D’où d=1,43 (2) mm et σ_d /d =1,36%)

{Remarque :

Avec les valeurs a= 72607488,97 V²/ Kg et σ_a = 2340324,52 V²/Kg données par Excel, nous obtenons d=1,402183E-03 m et σ_d = 2,269594E-05 m, i.e. d=1,40 (2) mm et σ_d /d =1,62% ; ici encore, les 2 « méthodes » ne s’opposent pas, puisque les 2 résultats se recouvrent. Nous choisissons le premier, encadré¹ci-dessus.}

Nous pouvons désormais déterminer C et σ_C :

C = e₀.S /d et σ_C = C*[(σ_d / d)² + (σ_l / l)² + (σ_L / L)²]^1/2

A.N. : C = 3,717857E-10 F et σ_C = 5,540797E-12 F

D’où C = 372 (6) pF

(¹Pour information, si nous calculons d et σ_d puis C et σ_{C ,} à partir des a et σ_a fournis par Excel, nous obtenons C = 379 (7) pF. Finalement, les deux valeurs de C se recouvrent également.)